LCM Word Problems with Answers

Looking for LCM (Least Common Multiple) word problems with answers? Explore a collection of engaging LCM word problems along with their solutions. Sharpen your math skills by solving these real-world scenarios involving finding the smallest common multiple. Get ready to ace your math exams with our comprehensive LCM word problem examples.

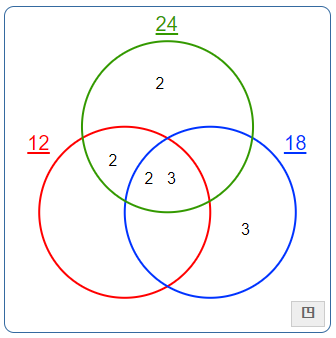
A baker needs to bake 12 dozen cookies, 18 dozen muffins, and 24 dozen cupcakes. What is the least number of cookies, muffins, and cupcakes that the baker needs to buy?

Solution: The least common multiple of 12, 18, and 24 is 72.

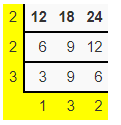
LCM = 2 x 2 x 3 x 3 x 2

LCM of 12, 18, 24 = 72

Therefore, the baker needs to buy at least 72 cookies, 72 muffins, and 72 cupcakes.

• LCM of 4, 7, 11
• LCM of 120. 180
• LCM of 12, 18

Least Common Multiple Word Prolems with Answers

Problem 1:
Johnny wants to arrange his comic books in stacks. He has 15 Batman comics and 12 Spider-Man comics. What is the least number of stacks he can make where each stack has the same number of comics?

Answer:
To find the LCM of 15 and 12, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 15: 15, 30, 45, 60, ...
Multiples of 12: 12, 24, 36, 48, 60, ...
So, the least common multiple (LCM) of 15 and 12 is 60. Johnny can make 60 stacks of comics.

Problem 2:
Sarah is planning a dance party. She wants to have balloons in sets of 8 and sets of 10. What is the least number of balloons she needs to buy to have an equal number of each set?

Answer:
To find the LCM of 8 and 10, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 8: 8, 16, 24, 32, 40, ...
Multiples of 10: 10, 20, 30, 40, ...
So, the least common multiple (LCM) of 8 and 10 is 40. Sarah needs to buy 40 balloons.

Problem 3:
A bakery sells cupcakes in boxes of 6 and boxes of 9. What is the least number of cupcakes they need to sell to have an equal number of each box?

Answer:
To find the LCM of 6 and 9, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 6: 6, 12, 18, 24, ...
Multiples of 9: 9, 18, 27, 36, ...
So, the least common multiple (LCM) of 6 and 9 is 18. The bakery needs to sell 18 cupcakes.

Problem 4:
Lily is organizing her toy cars. She has sets of 4 and sets of 7 cars. What is the least number of cars she needs to have an equal number of each set?

Answer:
To find the LCM of 4 and 7, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 4: 4, 8, 12, 16, 20, ...
Multiples of 7: 7, 14, 21, 28, ...
So, the least common multiple (LCM) of 4 and 7 is 28. Lily needs to have 28 cars.

Problem 5:
A classroom has 18 boys and 24 girls. The teacher wants to line them up in equal rows with the same number of boys and girls in each row. How many students will be in each row?

Answer:
To find the LCM of 18 and 24, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 18: 18, 36, 54, 72, ...
Multiples of 24: 24, 48, 72, ...
So, the least common multiple (LCM) of 18 and 24 is 72. There will be 72 students in each row.

Problem 6:
John is organizing a field trip for his classmates. He needs to rent buses that can fit 16 students or 20 students. What is the least number of buses he needs to rent to accommodate everyone?

Answer: To find the LCM of 16 and 20, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 16: 16, 32, 48, 64, 80, ...
Multiples of 20: 20, 40, 60, 80, ...
So, the least common multiple (LCM) of 16 and 20 is 80. John needs to rent 80 buses.

Problem 7:
Lisa has a collection of 30 marbles, and Alex has a collection of 45 marbles. They want to display their marbles together in such a way that each row has the same number of marbles. How many marbles will be in each row?

Answer: To find the LCM of 30 and 45, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 30: 30, 60, 90, 120, ...
Multiples of 45: 45, 90, 135, ...
So, the least common multiple (LCM) of 30 and 45 is 90. There will be 90 marbles in each row.

Problem 8:
A factory produces items in batches of 5 or 7. If they want to package the items in the same number per box, what is the least number of items per box they should use?

Answer: To find the LCM of 5 and 7, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 5: 5, 10, 15, 20, 25, 30, ...
Multiples of 7: 7, 14, 21, 28, 35, ...
So, the least common multiple (LCM) of 5 and 7 is 35. They should use 35 items per box.

Problem 9:
A farmer wants to divide his field into equal sections for planting crops. The field is 36 meters wide and 48 meters long. What is the least length of each section if the farmer wants them to be the same size?

Answer: To find the LCM of 36 and 48, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 36: 36, 72, 108, 144, ...
Multiples of 48: 48, 96, 144, ...
So, the least common multiple (LCM) of 36 and 48 is 144. Each section should have a length of 144 meters.

Problem 10:
Tom has a collection of 9 red marbles and 12 blue marbles. He wants to arrange them in a pattern where each row has the same number of marbles. How many marbles will be in each row?

Answer: To find the LCM of 9 and 12, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 9: 9, 18, 27, 36, 45, ...
Multiples of 12: 12, 24, 36, 48, ...
So, the least common multiple (LCM) of 9 and 12 is 36. There will be 36 marbles in each row.

Problem 11:
Maria has a collection of 10 stickers, and Jake has a collection of 16 stickers. They want to display their stickers together in such a way that each row has the same number of stickers. How many stickers will be in each row?

Answer: To find the LCM of 10 and 16, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 10: 10, 20, 30, 40, 50, ...
Multiples of 16: 16, 32, 48, 64, ...
So, the least common multiple (LCM) of 10 and 16 is 80. There will be 80 stickers in each row.

Problem 12:
Emily is planning a camping trip. She needs to pack enough supplies for 12 people, and each person needs 15 water bottles. What is the least number of water bottles Emily should pack?

Answer: To find the LCM of 12 and 15, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 12: 12, 24, 36, 48, 60, ...
Multiples of 15: 15, 30, 45, 60, ...
So, the least common multiple (LCM) of 12 and 15 is 60. Emily should pack 60 water bottles.

Problem 13:
Sara is making friendship bracelets. She wants to use strands of thread that are each 8 inches long and 12 inches long. What is the least length she can cut the thread so that each strand is the same size?

Answer: To find the LCM of 8 and 12, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 8: 8, 16, 24, 32, 40, ...
Multiples of 12: 12, 24, 36, 48, ...
So, the least common multiple (LCM) of 8 and 12 is 24. Sara should cut each strand to a length of 24 inches.

Problem 14:
A group of friends is planning a movie night. They want to buy popcorn that comes in bags of 3 cups and bags of 5 cups. What is the least number of cups of popcorn they need to buy to have an equal number of each bag?

Answer: To find the LCM of 3 and 5, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 3: 3, 6, 9, 12, 15, ...
Multiples of 5: 5, 10, 15, 20, ...
So, the least common multiple (LCM) of 3 and 5 is 15. They need to buy 15 cups of popcorn.

Problem 15:
A delivery truck can carry boxes that weigh 12 pounds or 18 pounds. What is the least weight each box should have if they want to load an equal number of each type of box?

Answer: To find the LCM of 12 and 18, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 12: 12, 24, 36, 48, ...
Multiples of 18: 18, 36, 54, ...
So, the least common multiple (LCM) of 12 and 18 is 36. Each box should have a weight of 36 pounds.

Problem 16:
Amy wants to create a pattern with colored tiles. She has tiles in sets of 4 and sets of 6. What is the least number of tiles she needs to use to have an equal number of each set in the pattern?

Answer: To find the LCM of 4 and 6, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 4: 4, 8, 12, 16, 20, ...
Multiples of 6: 6, 12, 18, 24, ...
So, the least common multiple (LCM) of 4 and 6 is 12. Amy needs to use 12 tiles.

Problem 17:
Daniel wants to arrange his toy cars in rows. He has 9 red cars and 15 blue cars. What is the least number of cars he can place in each row so that each row has the same number of cars?

Answer: To find the LCM of 9 and 15, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 9: 9, 18, 27, 36, ...
Multiples of 15: 15, 30, 45, ...
So, the least common multiple (LCM) of 9 and 15 is 45. Daniel can place 45 cars in each row.

Problem 18:
Alice is planning a school event. She needs to distribute 20 pens and 30 pencils equally among the students. What is the least number of students she can have?

Answer: To find the LCM of 20 and 30, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 20: 20, 40, 60, 80, ...
Multiples of 30: 30, 60, 90, ...
So, the least common multiple (LCM) of 20 and 30 is 60. Alice can have 60 students.

Problem 19:
Sarah wants to organize her bookshelf with books that come in sets of 5 and sets of 8. What is the least number of books she needs to have to have an equal number of each set?

Answer: To find the LCM of 5 and 8, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 5: 5, 10, 15, 20, 25, 30, ...
Multiples of 8: 8, 16, 24, 32, 40, ...
So, the least common multiple (LCM) of 5 and 8 is 40. Sarah needs to have 40 books.

Problem 20:
A group of friends is planning a road trip. They have two cars, and one car can travel 24 miles on a full tank, while the other car can travel 36 miles on a full tank. What is the least distance they need to travel so that both cars run out of gas at the same time?

Answer: To find the LCM of 24 and 36, we can list the multiples of each number and find the smallest multiple that they have in common.
Multiples of 24: 24, 48, 72, 96, ...
Multiples of 36: 36, 72, 108, ...
So, the least common multiple (LCM) of 24 and 36 is 72. They need to travel a distance of 72 miles for both cars to run out of gas at the same time.